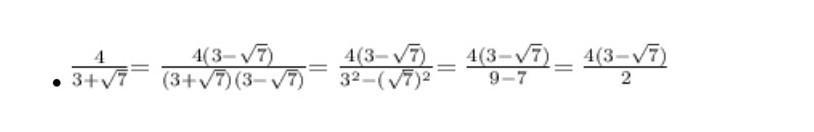How's your day 9 my way

Answers 1

Answer:

its good hbu

Explanation:

i dont know how i exokain

Do you know the answer? Add it here!

Can't find the answer?

Other related questions that may help you

Rationalize the denominator of the fraction below. What is the new denominator? [tex]\frac{4}{3+√7} \\ [/tex]​
question img

Answer:

Therefore, the new denominator will be 2

Step-by-step explanation:

To rationalize the denominator with a given square root, first thing we have to do is conjugate and also we can apply Difference of Two Square. In this way, the denominator will now be a rational number.

  • [tex] \boxed{\rm{Solution \ is \ attached.}} [/tex]

Therefore, the new denominator will be 2

answer img

Answer:

[tex] \large \boxed{\bold{2}}[/tex]

Step-by-step explanation:

[tex]\frac{4}{3 + \sqrt{7}} \\ [/tex]

Rationalise the denominator by multiplying the numerator & denominator of the fraction with [tex](3 - \sqrt{7})[/tex].

[tex]\frac{4\left(3-\sqrt{7}\right)}{\left(3+\sqrt{7}\right)\left(3-\sqrt{7}\right)} \\ [/tex]

Now, we an see that the denominator is in the form of the algebraic identity: (x + y) (x - y) = x² - y². So,

[tex]\frac{4\left(3-\sqrt{7}\right)}{3^{2}-\left(\sqrt{7}\right)^{2}} \\= \frac{4\left(3-\sqrt{7}\right)}{9-7} \\= \frac{4\left(3-\sqrt{7}\right)}{2} \\[/tex]

▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

Anong balita Ang kadalasan mong napapnood o naririnig

Answer:

Oil price hike

Explanation:

Dahil sa digmaan ng rusia at ukrain kaya tumaas ang petrolyu sa bansa

balitang pangkabuhayan

Explanation:

dahil ito kadalasan na ririnig natin na hinaiing dahil sa kakapusan Ng pera

paano nabuo ang rhymic pattern sa bawat measure ng awit ​

Answer:

NABUO ANG RHYMIC PATTERN SA BAWAT MEASURE NG AWIT UPANG MALAMAN ANG SUKAT NG ISANG AWIT AT KUNG MAGKATUNOG BA ITO O HINDI MAGKATUNOG KAYA NABUO ANG RHYMIC PATTERN.

paano nakatulong ang estratihikong lokasyon Ng pilipinas SA pag hubog Ng ating kasaysayan?​

Ang hubog nang kasaysayan at wla iba dahil dto

Other Chemistry Questions

Log in with Google

 or

Forgot your password?

I don't have an account, and I want to Register

Choose a language and a region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years