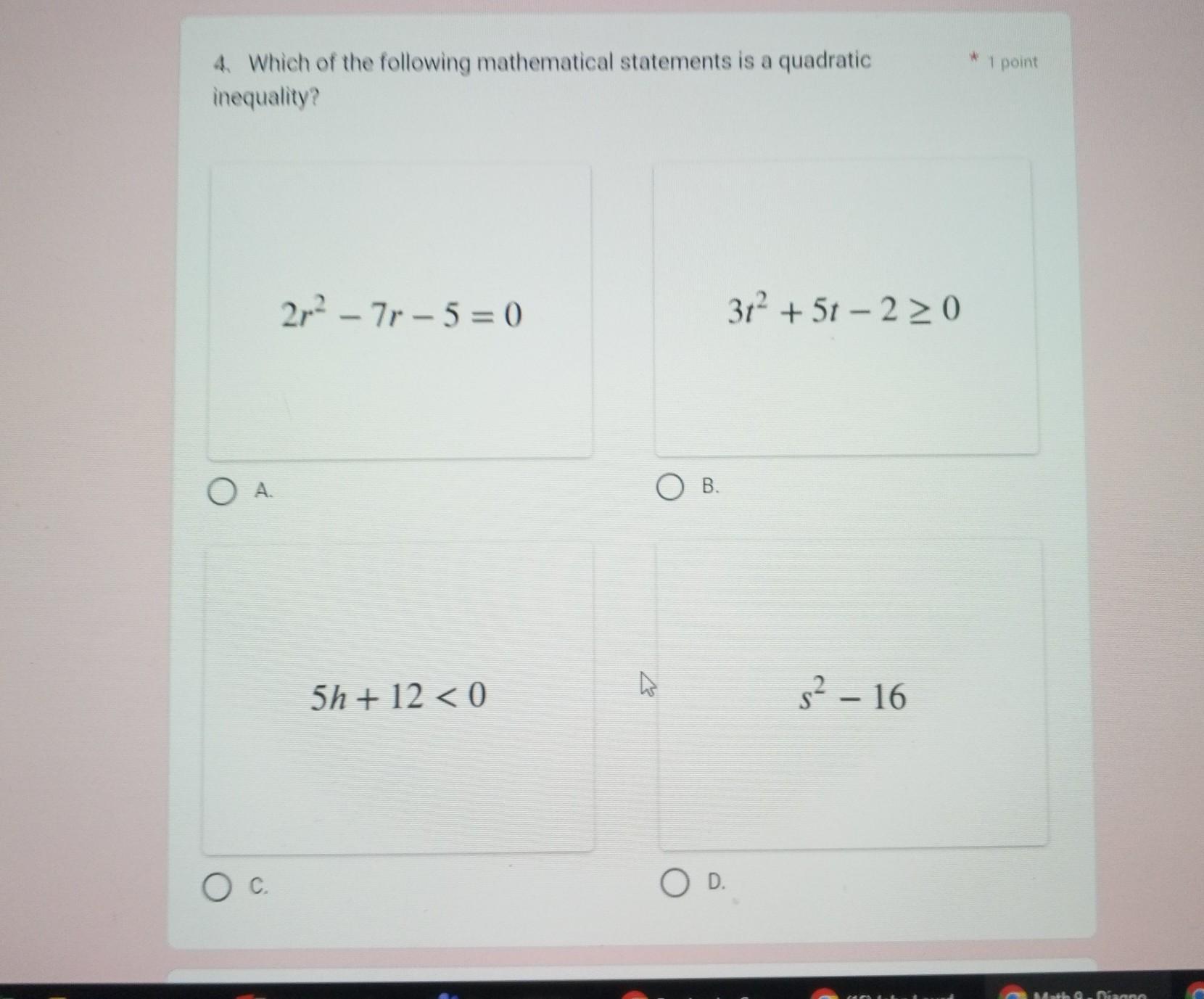
write 10 examples of analogy and identify its type
Answers 1
Answer:
Opposites Analogies. ...
Object and Classification Analogies. ...
Object and Related Object Analogies. ...
Object and Group Analogies. ...
Degrees of a Characteristic Analogies. ...
Cause and Effect Analogies. ...
Effort and Result Analogies. ...
Explanation:
Nakita ko lng
-
Author:
katowilcox
-
Rate an answer:
9
Do you know the answer? Add it here!
Choose a language and a region
How much to ban the user?
1 hour
1 day
100 years