2.Mgbigay ng tig 5 halimbawa ng karunungang bayan at ipaliwanag ang kahulugan nito.​

Step-by-step explanation:

hi good afternoon sir

Answer:

Hat = dog

Hotdog

2x2=hotdog

Answer:

3 ¾ will be 3 15/20

2 3/5 will be 2 12/20

5 ½ will be 5 10/20

Now proceed to addition, since all has the same denominator.

3 15/20+ 2 12/20+ 5 10/20= 10 37/20 or 11 17/20

Answer:

[tex] \qquad \large \bold{ (a) \: \: 30.2 \: m} \\ [/tex]

[tex] \qquad \large \bold{(b) \: \: 71.1 \: m} \\ [/tex]

Step-by-step explanation:

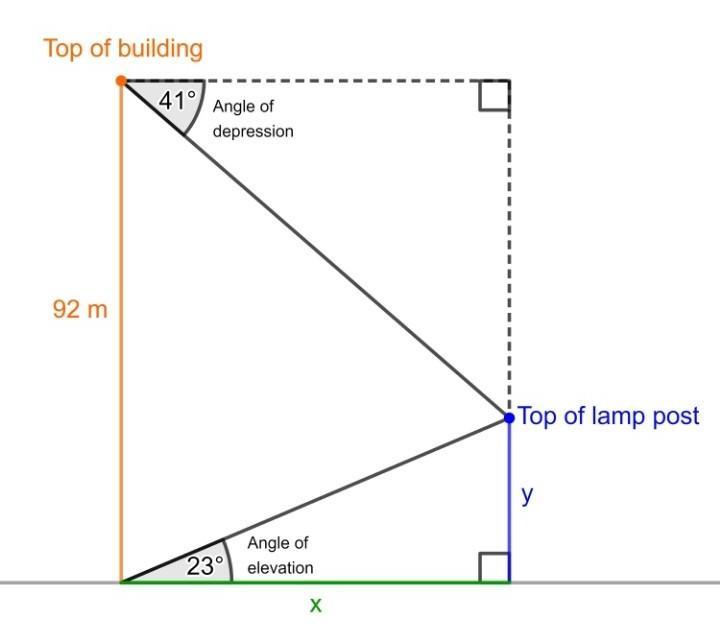
The given scenario can be modeled as two right triangles where the sum of their heights is 92 m (see attachment).

[tex] \\ \underline{ \sf{ \pmb{Define } \: the \: \pmb{variables}}} \\ [/tex]

• Let x = the distance between the foot of the building and the foot of the lamp post.
• Let y = the height of the lamp post.

Use the given information and the tan trigonometric ratio to create equations for the height of the lamp post.

[tex] \\ \underline{ \sf{ \pmb{Tan \: trigonometric \: ratio : }}} \\ [/tex]

[tex] \qquad \qquad \leadsto \: \sf \tan(\theta)=\dfrac{O}{A} \\ [/tex]

[tex] \sf{where:} \\ [/tex]

• [tex] \sf{ \pmb{\theta} \: is \: the \: \pmb{angle}} \\ [/tex]
• [tex] \sf{ \pmb{O} \: is \: the \: \pmb{side \: opposite} \: the \: \pmb{angle}} \\ [/tex]
• [tex] \sf{ \pmb{A } \: is \: the \: \pmb{side \: adjacent} \: of \: the \: \pmb{angle}} \\ [/tex]

[tex] \sf{For \: the \: \pmb{ angle } \: of \: \pmb{elevation \: triangle}:} \\ [/tex]

• [tex] \bold{ \theta = 23°} \\ [/tex]
• [tex] \bold{O = y} \\ [/tex]
• [tex] \bold{A = x} \\ [/tex]

[tex] \large \sf{Therefore:} \\ [/tex]

[tex]\implies \: \sf \tan(23^{\circ})=\dfrac{y}{x} \\ [/tex]

[tex]\implies \: \sf y=x\tan(23^{\circ}) \\ [/tex]

[tex] \sf{For \: the \: \pmb{ angle} \: of \: \pmb{depression \: triangle}:} \\ [/tex]

• [tex] \bold{ \theta = 41°} \\ [/tex]
• [tex] \bold{O = 92 - y} \\ [/tex]
• [tex] \bold{A = x} \\ [/tex]

[tex] \large \sf{Therefore:} \\ [/tex]

[tex]\implies \: \sf \tan(41^{\circ})=\dfrac{92-y}{x} \\ [/tex]

[tex]\implies \: \sf x\tan(41^{\circ})=92-y \\ [/tex]

[tex]\implies \: \sf y=92-x\tan(41^{\circ}) \\ [/tex]

Substitute the equation for the angle of elevation triangle into the equation for depression triangle and solve for x:

[tex]\implies \: \sf x\tan(23^{\circ})=92-x\tan(41^{\circ}) \\ [/tex]

[tex]\implies \: \sf x\tan(23^{\circ})+x\tan(41^{\circ})=92 \\ [/tex]

[tex]\implies \: \sf x[\tan(23^{\circ})+\tan(41^{\circ})]=92 \\ [/tex]

[tex]\implies \: \sf x=\dfrac{92}{\tan(23^{\circ})+\tan(41^{\circ})} \\ [/tex]

[tex]\implies \: \sf x=71.11047605. . . m \\ [/tex]

Therefore, the distance of the lamp post from the foot of the building is 71.1 m (nearest tenth).

To find the height of the lamp post, substitute the found value of x into one of the found equations for y:

[tex]\implies \: \sf y=x\tan(23^{\circ}) \\ [/tex]

[tex]\implies \: \sf y=\left(\dfrac{92 }{\tan(23^{\circ})+\tan(41^{\circ})}\right)\tan(23^{\circ}) \\ [/tex]

[tex]\implies \: \sf y=\dfrac{92 \tan(23^{\circ})}{\tan(23^{\circ})+\tan(41^{\circ})} \\ [/tex]

[tex]\implies \: \sf y=30.18460625. . .m \\\\ [/tex]

Therefore, the height of the lamp post is 30.2 m (nearest tenth).

Answer:

• A solution of salt water by mixing salt and water.

• Sugar water by mixing sugar in water.

• Mouthwash is a solution with lots of chemicals already mixed in it.

• Tincture of iodine can also be obtained by mixing crystals of iodine in alcohol.

• Vinegar is a solution which is formed by mixing acetic acid and water.

Explanation:

hope it helps

Answer:

what were the based of grouping the elements